还有不到20多天,2020年的农历春节就要到了。对于中国人来讲,农历春节是一年最隆重的节日。笔者曾经编写过农历计算的程序。为此调研过一段农历的算法。我国现行的农历,经过了若干次迭代,形成了如今的版本。农历,精确地反映了太阳、地球、月亮的天体运动的相对位置。2016年11月30日,农历中的二十四节气被正式列入联合国教科文组织人类非物质文化遗产名录。那么,农历是如何定义的,年份又是如何计算的,农历的月是如何划分的,二十四节气的天文学意义是什么以及如何用计算机推算农历?这篇文章将给大家做比较详细的解答。
古人将日月分别称为太阳和太阴,从常识我们了解到,每个月的农历十五日是月圆之日;初八前后,月亮东暗西明,称为上弦月;农历二十三前后,月亮西暗东明,称为下弦月。此外还有朔月、望月等等,我们可以看到,农历比较准确地反映了月相的变化。

习惯上,很多人会将我们的农历称为阴历。这实际是一种讹传。实际上,农历不仅可以反映月相的变化,同时,可以和现行广泛使用的太阳历(格里高利历,即现行公历)对应,反映地球绕太阳公转的相对位置以及寒暑变化。因此,农历实际是一种阴阳历。
由于历法有确切的天文学定义,同时要兼顾地球公转和月亮绕地球旋转的位置,历法会比公历稍显复杂,不过,掌握了农历,会对地月日运动关系有更深的理解,也是掌握潮汐变化、日月食预测等等的利器。
接下来,我们就来简单描述一下农历的历法:
- 以东八区北京时间为标准时间。
- 地球自转一周的时间约为一天;月亮月相变化的一个周期为一个月;地球绕太阳旋转一周约为一年。
- 每个朔日即无法看见月亮的日期为每月起点,即初一。
- 包含冬至的月份为十一月,也即冬月。
- 相邻两个冬月之间为一年。
- 冬月后的第二个非闰月,为正月。
- 将没有中气的那个朔望月置为闰月。
规则较为繁复,我们依次来解说之。
由于地球自转,世界各地时刻不一致。现行的中国农历习惯上以北京时间(东经120度经线所在时刻)作为参考,而1929年以前的阴历,则以北京即东经116度25分的当地时为准。实际上,根据农历的法则可以选用任意的地理位置,如越南和韩国都使用农历,但参考位置不同。
地球自转一周时间约为23时56分4秒;月相变化周期约为29.530589天,因此,农历有大小月之分,大月30天,小月29天;地球绕太阳公转一周的时间约为365.256363004天,每年会有一定的误差,因此,各种历法都考虑了闰年的方案。现行的公历(格里高利历),采用每4年增加一个闰日,同时对整百年,取消3次闰年,使得历法与公转年近似一致。我们的农历现行使用19年7闰的方式来进行调整,原理在于365.256363004/29.530589约等于12.368746285554954也即一个回归年要多出0.368746285554954个月。将其乘以19,得到7.006179425544126。这也即19年7个闰月的原理。与公历不同,农历的闰,是闰一个月。比如2020年的闰四月就整整闰出29天。
农历的纪年比较有特色,使用天干和地支进行搭配来达到计数的目的。
天干为:甲乙丙丁戊己庚辛壬癸;地支为:子丑寅卯辰巳午未申酉戌亥。
每一年由天干按顺序选出一位,地支按顺序选出一位,和为干支纪年。古人常用这种方式来描述年份,如王羲之的《兰亭集序》中“永和九年,岁在癸丑”。
每一个干支纪年周期以甲子为始,以癸亥为终,癸亥之后再从甲子开始。有副对联描述这个现象:“一岁两春双八月人间两度春秋,六旬花甲再周天世上重逢甲子”。上联说的是闰八月,下联讲的就是纪年周期。
为了便于记忆,人们还给十二地支配以十二个动物生肖,所以有:子鼠丑牛寅虎卯兔辰龙巳蛇午马未羊申猴酉鸡戌狗亥猪。因此,2020年就是农历庚子鼠年。

下面的代码可以实现农历年转干支年:
const Heavenly = "甲乙丙丁戊己庚辛壬癸"
const Earthly = "子丑寅卯辰巳午未申酉戌亥"
const Zodiac = "鼠牛虎兔龙蛇马羊猴鸡狗猪"
const YearHeavenlyDelta = 6
const YearEarthlyDelta = 8
const yearHeavenlyIdx = year => (year + YearHeavenlyDelta) % Heavenly.length
const yearEarthlyIdx = year => (year + YearEarthlyDelta) % Earthly.length
const year2HE = year => {
let earthlyIdx = yearEarthlyIdx(year)
return {
heavenly: Heavenly[yearHeavenlyIdx(year)],
earthly: Earthly[earthlyIdx],
zodiac: Zodiac[earthlyIdx]
}
}
上述代码可以通过调用year2HE(year)查询农历年的干支和生肖。
除了干支纪年,人们也用干支记录月与日。如1949年10月1日为:己丑年癸酉月甲子日。循环方式与纪年法无异。同样是周期为60的周期函数。
对于闰月,干支与前一个月相同,所以每年月的地支是固定的。天干的公式为:取公历年份除以5的余数减2后乘以2再减2,当该数是负数时加10。需要说明的是,因为农历以冬月(十一月)建子(为子月),因此月的地支正月为寅,二月为卯,…… ,腊月为丑。下面的代码可以计算月干支:
const monthHeavenlyIdx = (year, month)=> {
let ret = ((year % 5) - 2) * 2 - 2
return ret < 0 ? ret + 10 : ret
}
const month2HE = (year, month) => {
return {
heavenly: Heavenly[monthHeavenlyIdx(year, month)],
earthly: (Earthly.split("").join("").replace("子丑", "") + "子丑").split("")[month - 1]
}
}
同样地,人们常用地支来标注时辰。从子时到亥时,依次分别对应23时到1时,1时到3时,...,21时到23时。所以,你看《长安十二时辰》时候,就知道大致是几点了。
如果是公历的话,需要先转化成农历,然后再调用这些方法来判断干支。文章结尾的地方,我会给读者推荐一个这样的库。
农历的月份划分是以朔日作为标准的。朔日,即当天月球恰好运行至与太阳黄经相等,称为朔。月球运行到地球和太阳之间,和太阳几乎同时出没,在地球上看不到月亮。朔日也是经常发生日食的时候。
在上面的规则中,我们发现,农历定准的起点是冬至所在的月。那么为什么会以冬至作为标准呢?古代对于日相的观测,是以日影长短作为标志的,而冬至日是正午日影最长的那一天。这个观测是最为简便和准确的,按天文学定义,即是太阳黄道经270度所在的日期,因此冬至日成为了农历计算时最重要的参照物。
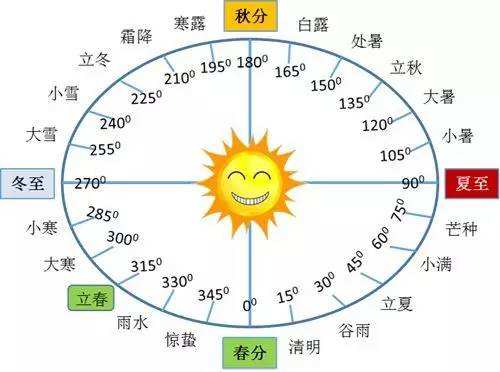
定出了起点,下面就是二十四节气的舞台了,与反映月相变化不同,二十四节气则是反映地球绕太阳公转的位置,也即通常意义的寒暑变化。这是农历是阴阳合历的重要佐证。所谓“节”和“气”是独立的概念。一年中的十二节和十二气合为二十四节气。下图是平年中二十四节气与农历十二个月的分布关系。
一般情况下,一个农历月包含一个“节”和一个“气”。“节”又称为节令,“气”又称为“中气”。现行农历中,把不包含中气的月置闰。巧合的是,19年中的无中气月恰好为7个,因此,中气置闰法完美地解决了置闰难题。同时,由于是根据自然形成,并非人为指定。所以该方法还较好地反映了天体运行的规律。德国天文学家总结的开普勒三大定律告诉我们,地球绕太阳公转的轨道近似是一个椭圆形,太阳近似位于椭圆轨道的焦点。当北半球夏至前后,地球位于远日点。从太阳到行星所联接的直线在相等时间内扫过同等的面积。因此,位于远日点的地球此时角速度变慢,所以在一个月中出现无中气现象的概率大大增加。所以我们看到的闰月常常分布在年中这几个月,而绝少出现在年首和年尾。
除了二十四节气,农历中还有数九和伏天的规则。
数九的规则比较简单:以冬至为一九第一天,每9天为一个周期。第十天为二九第一天,依次类推。经过八十一天,即在惊蛰与春分之间,表示冬去春来。
伏天的计算稍复杂一些,会用到之前提到的干支法来记日。自夏至开始,依照干支纪日的排列,第3个庚日为初伏,第4个庚日为中伏,立秋后第1个庚日为末伏。例如:2020年的夏至日为公历:6月21日,当日为乙未日,则初伏需要按顺序找到第3个庚日,我们看到公历7月16日为庚申日。因此初伏第一天为公历2020年7月16日。根据定义,初伏一般都为十天,因此,7月26日庚午日为中伏第一天。而8月15日是立秋后第一个庚日:庚寅日。由于立秋的日期和干支日的配合,中伏可为10天或20天。
数九或者伏天,是从寒至暖或是从暑热到清凉的过渡。这里无论以九作为进制还是用十作为单位,人为规定的意义都要大于其天文学的含义。
农历的推算,在早年只能通过观测和数据整理推算,而每一年的农历均由官方发布。虽然理论比较完美,但限于技术和计算知识的匮乏,不准确的情况时有发生。历史上也有多次修改历法的记载。
比较著名的一次修改历法,是明代崇祯年间,徐光启吸收利玛窦带来的西方的天文学知识,由徐光启、李之藻等人编写的《崇祯历书》。这套历法与现行的农历比较接近,也比较好的满足了农历历法所提出的需求。只可惜,此历书未及推广,崇祯皇帝就出了神武门,去了景山。清代早期,汤若望对《崇祯历书》进行了删改、压缩,更名为《西洋新法历书》,并进呈清政府后,才被采用并改名《时宪历》正式颁行。辛亥革命之后,中华民国计划逐步废弃农历,代以西方的格里高利历,同时辅以民国XX年纪年,不过民间应者寥寥,遂公历、农历并用。中华人民共和国成立时,继续使用公历,以公元纪年,但保留中国传统历——夏历的使用,并于公元2017年颁布了国家标准《农历的编算和颁行》。1970年以后“夏历”改称为“农历”。现行农历由中国科学院紫金山天文台负责计算,属于官方历书《中国天文年历》的组成部分。
1982年,P.Bretagnon公开发表了VSOP行星理论,该理论的英文名称是:Secular Variations of the Planetary Orbits,VSOP的缩写其实是源于法文名称:Variations Séculaires des Orbites Planétaires。VSOP理论是一个描述太阳系行星轨道在相当长时间范围内周期变化的半分析(semi-analytic)理论。
VSOP82理论是VSOP理论的第一个版本,提供了对太阳系几大行星位置计算的周期序列,通过对周期序列进行正弦或余弦项累加求和,就可以得到这个行星在给定时间的轨道参数。不过VSOP82由于每次都会计算出全部超高精度的轨道参数,这些轨道参数对于历法计算这样的民用场合很不适用。1987年,Bretagnon 和 Francou 创建了VSOP87行星理论,VSOP87行星理论不仅能计算各种精密的轨道参数,还可以直接计算出行星的位置,行星位置可以是各种坐标系,包括黄道坐标系。VSOP87行星理论由6张周期项系数表组成,分别是VSOP87、VSOP87A、VSOP87B、VSOP87C、VSOP87D和VSOP87E,其中VSOP87D表可以直接计算行星日心黄经(L)、日心黄纬(B)和到太阳的距离(R),此表计算出的结果适用于节气位置判断。
1991年,Jean Meeus出版了《Astronomical Algorithms》一书,详细介绍了计算机描述天文学的算法,包括了VSOP87算法#VSOP87)。
2008年,许剑伟老师将《Astronomical Algorithms》翻译成了中文版,为推广计算机推算天体位置、天文现象打下了基础,并依此写出了早期的包含农历的万年历版本。
这些算法,有多种语言的实现版本,如golang的Meeus、以及对应的NodeJS实现。
由于农历上朔日的推算决定了每个月究竟有多少天,以及每个农历日的干支纪日的干支。VSOP87给计算机直接计算农历相关问题的方案。相关的行星数据需要从一定的资料网站下载。如:ftp://cdsarc.u-strasbg.fr/pub/cats/VI/81就是斯特拉斯堡大学的天文观测数据。
在此基础上,有一个JavaScript库,可以满足日常的农历推算需求。读者可以从这里了解其实现细节。作为API,该库提供了农历与公历互转、查询某年某节气、查询某年春节,以及和韩国、越南农历互转的方法。

Comments